Komposisi Fungsi dan Invers Fungsi
Komposisi Fungsi dan Invers Fungsi
Pengertian Fungsi Komposisi
Apa itu fungsi komposisi? Pengertian dari Fungsi komposisi adalah suatu penggabungan dari operasi dua jenis fungsi f(x) dan g(x) sehingga nantinya dapat menghasilkan fungsi yang baru.
Rumus Fungsi Komposisi
Operasi untuk fungsi komposisi ini pada umumnya dilambangkan dengan huruf atau simbol “o”. Lambang tersebut bisa dibaca komposisi atau bisa juga bundaran. Fungsi baru inilah yang bisa terbentuk dari f(x) dan juga g(x) yakni:
- (f o g)(x) artinya adalah g dimasukkan ke f
- (g o f) (x) artinya adalah f dimasukkan ke g
Fungsi tunggal merupakan salah satu fungsi yang dapat dilambangkan dengan huruf “f o g” atau bisa pula dibaca dengan “f bundaran g”. Selanjutnya untuk Fungsi ( f o g) (x) → f (g (x)) dapat dikomposisikan menjadi fungsi f (x).
Sementara itu, untuk “g o f” dapat dibaca sebagai fungsi g bundaran f. Sehingga “g o f” merupakan fungsi f yang harus diselesaikan terlebih dahulu dari fungsi g. Supaya memudahkan Anda dalam memahami mengenai materi fungsi ini, silahkan Anda perhatikan gambar berikut ini:
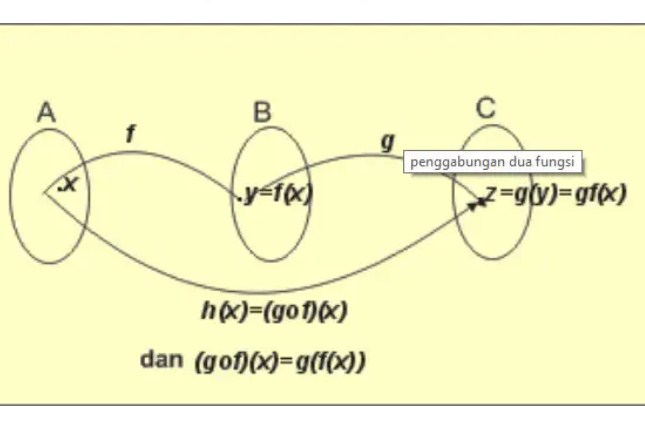
Dilihat dari skema rumus diatas maka bisa diketahui bahwa :
Apabila f : A → B maka ditentukan dengan menggunakan rumus y = f(x)
Apabila g : B → C maka ditentukan dengan menggunakan rumus y = g(x)
Jadi akan diperoleh suatu hasil fungsi g dan juga f, yaitu:
h(x) = (gof)(x) = g( f(x))
Dari definisi tersebut maka bisa kita ambil kesimpulan bahwa fungsi yang melibatkan antara fungsi f dengan g bisa ditulis seperti berikut ini:
- (g o f)(x) = g(f(x))
- (f o g)(x) = f(g(x))
Sifat-Sifat Fungsi Komposisi

Ternyata ada banyak sekali sifat yang dimiliki oleh fungsi komposisi. Adapun sifat-sifat pada fungsi komposisi adalah sebagai berikut ini:
Apabila f : A → B , g : B → C , h : C → D, maka akan berlaku berbagai sifat seperti berikut ini:
- (f o g)(x)≠(g o f)(x). Tidak berlaku sifat komutatif
- [f o (g o h)(x)] = [(f o g ) o h (x)]. bersifat asosiatif
- Apabila fungsi identitas I(x), maka nantinya akan berlaku (f o l)(x) = (l o f)(x) = f(x)
Contoh Soal Fungsi Komposisi

Fungsi Komposisi dalam Kehidupan
Selanjutnya kami akan menjelaskan mengenai fungsi komposisi dalam kehidupan sehari-hari, diantaranya:
- Pembuatan sebuah buku bisa diproses dengan melalui dua tahap, yakni:
- Pertama adalah tahap editorial yang nantinya akan dilanjutkan dengan tahap produksi.
- Dalam tahap editorial ini maka semua naskah akan di edit dan di layout untuk menjadi file yang sudah siap untuk di cetak.
- Selanjutnya adalah tahap produksi yang dimana file tersebut segera dicetak supaya menjadi sebuah buku.
- Untuk proses dalam pembuatan buku ini telah menerapkan algoritma fungsi komposisi.
- Untuk mendaur ulang logam, yakni:
- Awal mulanya pecahan logam campuran akan dijadikan sebagai serpihan kecil.
- Kemudian Drum magnetic yang ada di dalam mesin penghancur harus menyisihkan logam magnetic dengan memuat unsure bes.
- Selanjutnya untuk sisa pecahan logam harus segera dikeruk dan dipisahkan. Sementara untuk serpihan besi harus dilebur langsung menjadi baja yang baru. Proses dalam daur ulang logam ini menggunakan fungsi komposisi.
Fungsi Invers

Fungsi invers bisa terjadi karena adanya sebuah fungsi yang dinotasikan dengan f (x) dan memiliki relasi pada setiap himpunan A ke setiap himpunan B. Dengan demikian akan menjadi suatu fungsi invers dan dinotasikan dengan f-1 (x) yang tak lain mempunyai sebuah relasi dari himpunan B ke setiap himpunan A.
Jadi fungsi invers yang telah didapatkan dari f : A → B akan mengalami perubahan menjadi f-1 B → A sehingga untuk daerah asal atau domain f (x), berubah menjadi sebuah daerah kawan atau kodomain menjadi daerah hasil atau range f-1 (x) yakni himpunan A. Demikian pula sebaliknya yang terjadi pada himpunan B.
Fungsi invers atau yang biasa disebut dengan fungsi kebalikan merupakan suatu fungsi yang berkebalikan dari fungsi asalnya.
Sebuah fungsi f dapat dikatakan memiliki fungsi invers (kebalikan) f-1 apabila f merupakan fungsi satu-satunya dan fungsi pada (bijektif). Untuk hubungan tersebut dapat dinyatakan dengan rumus sebagai berikut ini:
(f-1)-1 = f
Secara umum bisa disimpulkan bahwa fungsi bijektif akan berlangsung ketika jumlah anggota domain sudah sama dengan jumlah anggota kodomain.
Setidaknya sekitar dua atau lebih domain yang berbeda dipetakkan kedalam domain yang sama. Untuk setiap kodomain memiliki pasangan pada domain. Untuk lebih jelasnya silahkan Anda perhatikan gambar di bawah ini.
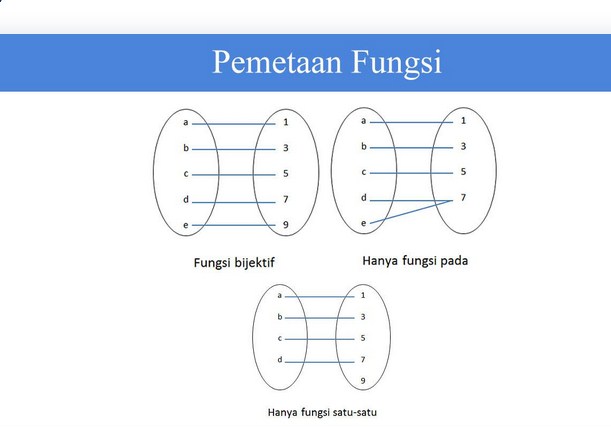
Menurut gambar dari gambar pemetaan tersebut, pemetaan yang pertama telah menunjukkan fungsi bijektif. Tetapi untuk pemetaan yang kedua bukan termasuk fungsi bijektif karena pemetaan diatas hanya berlangsung fungsi pada.
Untuk domain d dan juga e dipetakkan ke anggota kodomain yang tidak berbeda. Pemetaan yang ketiga juga bukan merupakan fungsi bijektif karena pemetaan diatas hanya akan berlangsung pada fungsi satu-satu. Kodomain 9 tidak memiliki pasangan sama sekali pada anggota domain.
Cara Mencari Invers dari Suatu Fungsi
Untuk mencari fungsi y=f(x) bisa dicari dengan cara sebagai berikut ini:
- Mengubah persamaan y=f(x) menjadi bentuk x=f(y)
- Menuliskan x dengan f-1(y) sehingga f(y) = f-1(y)
- Mengubah variabel y dengan x sehingga akan diperoleh invers dari f(x) berupa f-1
Contoh Soal Fungsi Invers

Komentar
Posting Komentar