Soal Pertidaksamaan Kuadrat - Linear dan Kuadrat - Kuadrat

Nama : Hanna Kamila M. (16)

Kelas : X IPS 3


Soal Pertidaksamaan Kuadrat - Linear dan Kuadrat - Kuadrat


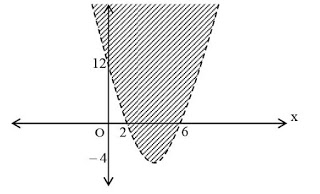
1. Gambarlah daerah penyelesaian pertidaksamaan kuadrat y > x2 – 8x + 12

Jawab

(1) Tititk potong dengan sumbu-X syarat y =0

x2 – 8x + 12 = 0

(x – 6)(x – 2) = 0

x = 6 dan x = 2 Titik potongnya (2, 0) dan (6,0)


(2) Tititk potong dengan sumbu-Y syarat x =0

y = x2 – 8x + 12

y = (0)2 – 8(0) + 12

y = 12 Titik potongnya (0, 12)


(3) Menentukan titik minimum fungsi y = x2 – 8x + 12

(4) Gambar daerah penyelesaiannya (Daerah yang diarsir adalah daerah penyelesaian)

2. Gambarlah daerah penyelesaian dari sistem pertidaksamaan 2x + 3y ≥ 12 dan y ≤ –x2 + 2x + 8 dalam tata koordinat Cartesius,

Jawab:

   Pertama akan digambar daerah penyelesaian 2x + 3y ≥ 12


   Selanjutnya digambar juga daerah penyelesaian y ≤ –x2 + 2x + 8, dengan langkah langkah :

   Menentukan tititk potong dengan sumbu-X syarat y = 0

–x2 + 2x + 8 = 0

x2 – 2x – 8 = 0

(x – 4)(x + 2) = 0

x = –2 dan x = 4 . 

     Titik potongnya (–2 0) dan (4, 0)

   Menentukan tititk potong dengan sumbu-Y syarat x = 0

y = –x2 + 2x + 8

y = –(0)2 + 2(0) + 8

y = 8 . Titik potongnya (0, 8)

Menentukan titik maksimum fungsi y = –x2 + 2x + 8




Menggambar daerah penyelesaiannya (Daerah yang diarsir adalah daerah penyelesaian)


Irisan dari kedua daerah penyelesaian tersebut merupakan penyelesaian dari sistem pertidaksamaan 2x + 3y ≥ 12 dan y ≤ –x2 + 2x + 8


Gambar daerahnya adalah sebagai berikut


4. Gambar daerah penyelesaian pertidaksamaan y ≤ –x2 + 6x – 8 .

(1) Tititk potong dengan sumbu-X syarat y =0

–x2 + 6x – 8 = 0

x2 – 6x + 8 = 0

(x – 4)(x – 2) = 0

x = 4 dan x = 2

Titik potongnya (4, 0) dan (2, 0)

(2) Tititk potong dengan sumbu-Y syarat x =0

y = –x2 + 6x – 8

y = –(0)2 + 6(0) – 8

y = –8

Titik potongnya (0, –8)

(3) Menentukan titik maksimum fungsi y = –x2 + 6x – 8



(4) Gambar daerah penyelesaiannya

(Daerah yang diarsir adalah daerah penyelesaian)


Daerah penyelesaian kedua pertidaksamaan itu adalah irisan dua daerah penyelesaian masing-masing pertidaksamaannya, yakni:


5. Gambarlah kedua pertidaksamaan kuadrat berikut ini dalam satu sistem koordinat Cartesius, kemudian tentukan daerah penyelesaiannya

y > x2 – 9

y ≤ –x2 + 6x – 8


Jawab : 


a. Gambar daerah penyelesaian pertidaksamaan y > x2 – 9


(1) Tititk potong dengan sumbu-X syarat y =0

x2 – 9 = 0

(x + 3)(x – 3) = 0

x = –3 dan x = 3

Titik potongnya (–3, 0) dan (3, 0)


(2) Tititk potong dengan sumbu-Y syarat x =0

y = x2 – 9

y = (0)2 – 9

y = –9

Titik potongnya (0, –9)


(3) Menentukan titik minimum fungsi y = x2– 9


(4) Gambar daerah penyelesaiannya

(Daerah yang diarsir adalah daerah penyelesaian)

Komentar

Posting Komentar

Postingan populer dari blog ini

Perbandingan Trigonometri pada Segitiga Siku-siku

Gambar
Nama : Hanna Kamila M. (17) Kelas : X IPS 3 Tanggal : 18 Januari 2021 Perbandingan Trigonometri pada Segitiga Siku-siku Trigonometri  dapat dikatakan sebagai suatu cabang ilmu matematika yang mempelajari mengenai sudut, sisi, dan perbandingan antara sudut terhadap sisi. Menurut bahasanya, trigonometri berasal dari bahasa Yunani.  Trigonon  yang berarti tiga sudut, dan  metro  yang berarti mengukur. Dalam pembahasan mengenai trigonometri, kita akan banyak menggunakan sifat-sifat bangun datar segitiga. Teorema apa yang dipakai untuk menentukan panjang sisi segitiga siku-siku yang belum diketahui? Yak betul, kita akan menggunakan teorema/dalil pythagoras. Pythagoras  adalah seorang matematikawan asal Yunani yang dikenal dengan teoremanya,  yaitu bahwa sisi miring atau sisi terpanjang dalam segitiga siku – siku sama dengan jumlah kuadrat sisi – sisi lainnya. Pada gambar segitiga ABC di atas, AC merupakan sisi miring ( hipotenusa ) sehingga berlaku teorema pythagoras: AC² = AB² + BC² Perban
Baca selengkapnya

Pengukuran Sudut

Gambar
Nama : Hanna Kamila M. (17) Kelas : X IPS 3 Tanggal : 11 Januari 2021 Pengukuran Sudut 1. Pengertian Sudut Sebelum memasuki materi pengukuran sudut mari kita ketahui dulu apa pengertian dari sudut. Sudut yaitu daerah yang dibatasi dua garis lurus atau dua sinar atau sudut  yang dapat kita gambarkan sebagai pertemuan dua garis lurus. Dalam kehidupan sehari-hari kita tentunya akan banyak menemukan sudut, lihat lah di sekitar kalian. Mari kita perhatikan gambar benda di bawah ini. Membandingkan besar dua sudut Bagaimana membandingkan dua sudut? Dan dapatkah kalian membandingkan sudut mana yang lebih besar dan sudut mana yang lebih kecil? Mari kita lakukan beberapa praktik membandingkan dua buah sudut. Pertama lihat dua buah sudut dibawah ini : Selanjutnya gabungkan kedua sudut tersebut dengan menghimpitkan kedua sudut dengan salah satu garis saling menempel. Lihat gambar dibawah ini. Lihat kamu dapat membedakan yang mana sudut yang lebih besar dan yang mana sudut yang lebih kecil. Dari pr
Baca selengkapnya

Sudut-Sudut Berelasi pada Kuadran I, II, III, IV

Nama : Hanna Kamila M. (17) Kelas : X IPS 3 Tanggal : 8 Februari 2021 SUDUT-SUDUT BERELASI PADA KUADRAN I, II, III, IV Sudut Berelasi merupakan lanjutan dari ilmu trigonometri tentang kesebangunan pada segitiga siku-siku untuk sudut kuadran I atau sudut lancip (0 − 90°). Mari kita simak penjelasannya berikut. Rumus Sudut Berelasi Dengan memanfaatkan sudut-sudut relasi, kita dapat menghitung nilai perbandingan pada trigonometri untuk sudut pada kuadran lainnya, termasuk sudut yang lebih dari 360° dan sudut negatif. Sudut Berelasi di Kuadran I Untuk α = sudut lancip, maka (90° − α) merupakan sudut-sudut kuadran I. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut : sin (90° − α) = cos α cos (90° − α) = sin α tan (90° − α) = cot α Sudut Berelasi di Kuadran II Untuk α = sudut lancip, maka (90° + α) dan (180° − α) merupakan sudut-sudut kuadran II. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut : sin (90° + α) = cos α cos (90° + α) = -sin α tan (90° + α) = -cot α sin (
Baca selengkapnya