Soal dan Pembahasan Fungsi Trigonometri

Nama : Hanna Kamila M. (17)
Kelas : X IPS 3
Tanggal : 5 April 2021 

SOAL DAN PEMBAHASAN FUNGSI TRIGONOMETRI

Soal Nomor 1
Diketahui grafik fungsi $y_1=5\sin x$ dan $y_2=\sin 5x$. Pernyataan berikut yang benar adalah $\cdots \cdot$
A. periode $y_1$ = periode $y_2$
B. amplitudo $y_1$ = amplitudo $y_2$
C. periode $y_1=\frac{1}{5}$ kali periode $y_2$
D. amplitudo $y_1=\frac{1}{5}$ kali amplitudo $y_2$
E. amplitudo $y_1=5$ kali amplitudo $y_2$

Pembahasan

Bentuk umum fungsi sinus tersebut adalah $y=a\sin kx$.
Periode:
Periode $y_1=5\sin x$ dengan $k=1$ adalah $P_1=\frac{{360}^{\circ }}{1}={360}^{\circ }$, sedangkan periode $y_2=\sin 5x$ dengan $k=5$ adalah $P_2=\frac{{360}^{\circ }}{5}={72}^{\circ }$.
Dapat disimpulkan bahwa periode $y_1$ sama dengan 5 kali periode $y_2$.
Amplitudo:
Amplitudo $y_1=5\sin x$ dengan $a=5$ adalah $A_1=|a|=|5|=5$, sedangkan amplitudo $y_2=\sin 5x$ dengan $a=1$ adalah $A_2=|a|=|1|=1$. Dapat disimpulkan bahwa amplitudo $y_1$ 5 kali amplitudo $y_2$.
Pernyataan yang benar ada pada pilihan E.

[collapse]

Soal Nomor 2
Grafik $f\left(x\right)=2\cos x$ memotong sumbu-$X$ di titik berkoordinat $\cdots \cdot$
A. $({30}^{\circ },0)$              D. $({90}^{\circ },0)$
B. $({45}^{\circ },0)$              E. $({180}^{\circ },0)$
C. $({60}^{\circ },0)$

Pembahasan

Apabila grafik memotong sumbu-$X$, maka nilai $f\left(x\right)=y=0$. Dengan demikian,
$f\left(x\right)=2\cos x\Rightarrow 0=2\cos x\iff \cos x=0$
Nilai $x$ yang membuat $\cos x$ bernilai 0 adalah ${90}^{\circ }$.
Jadi, titik potong grafiknya berkoordinat $({90}^{\circ },0)$
(Jawaban D)

[collapse]

Soal Nomor 3
Grafik di atas adalah grafik fungsi $\cdots \cdot$

A. $f\left(x\right)=\frac{1}{2}\sin \frac{1}{2}x$
B. $f\left(x\right)=\frac{1}{2}\sin 2x$
C. $f\left(x\right)=\frac{1}{2}\cos 2x$
D. $f\left(x\right)=2\cos \frac{1}{2}x$
E. $f\left(x\right)=2\cos 2x$

Pembahasan

Perhatikan sketsa gambar berikut.

Grafik di atas merupakan modifikasi grafik cosinus (karena grafiknya dimulai dari sumbu-$Y$) dengan bentuk umum $f\left(x\right)=a\cos kx$.
Grafik juga menunjukkan bahwa nilai maksimum fungsinya $\frac{1}{2}$, sedangkan nilai minimumnya $-\frac{1}{2}$, sehingga
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{\frac{1}{2}-(-\frac{1}{2})}{2}=\frac{1}{2}\end{array}$
Saat $x=0^{\circ }$, nilai fungsinya $\frac{1}{2}$, lalu berulang kembali di $x=\pi$, sehingga periodenya $\pi$. Dengan demikian, $k=\frac{2\pi }{\text{Periode}}=\frac{2\pi }{\pi }=2$.
Jadi, grafik fungsi di atas adalah grafik fungsi $f\left(x\right)=\frac{1}{2}\cos 2x$
(Jawaban C)

[collapse]

Soal Nomor 4
Grafik di atas adalah grafik fungsi $\cdots \cdot$

A. $y=2\sin x,0^{\circ }\le x\le {270}^{\circ }$
B. $y=2\cos 4x,0^{\circ }\le x\le {270}^{\circ }$
C. $y=4\sin 2x,0^{\circ }\le x\le {270}^{\circ }$
D. $y=4\cos 2x,0^{\circ }\le x\le {270}^{\circ }$
E. $y=4\sin 4x,0^{\circ }\le x\le {270}^{\circ }$

Pembahasan

Perhatikan sketsa gambar berikut.

Beranjak dari grafik sinus yang memiliki bentuk umum $f\left(x\right)=a\sin kx$, kurva pada gambar tidak bergeser dan berawal dari titik $(0,0)$. Grafik juga menunjukkan bahwa nilai maksimum dan minimum fungsi adalah $4$ dan $-4$, sehingga
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{4-(-4)}{2}=4\end{array}$
Pada saat nilai $x={180}^{\circ }$, fungsi kembali bernilai $0$, lalu berulang kembali seperti sebelumnya, sehingga periodenya adalah ${180}^{\circ }$, dan akibatnya
$k=\frac{{360}^{\circ }}{{180}^{\circ }}=2$
Jadi, rumus fungsi $f\left(x\right)=4\sin 2x$ dengan batas interval $0^{\circ }\le x\le {270}^{\circ }$
(Jawaban C)

Soal Nomor 5

Grafik fungsi 

$f\left(x\right)=-2\cos 3x,-\pi \le x\le \pi$ adalah $\cdots \cdot$

Pembahasan

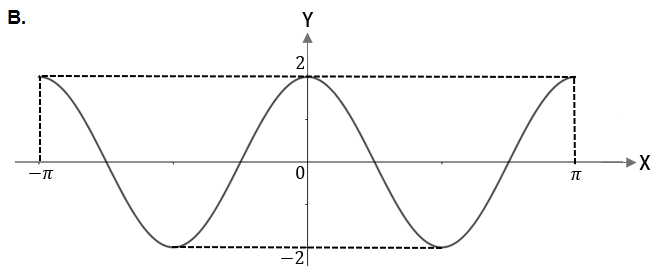
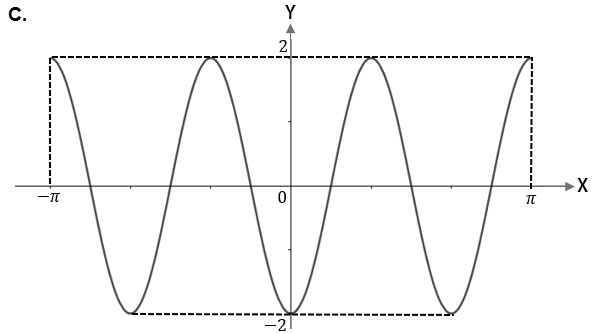
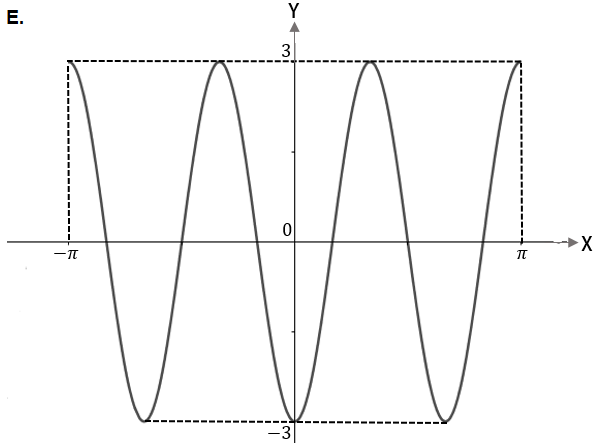
Bentuk umum fungsi cosinus adalah $f\left(x\right)=a\cos kx$. Oleh karena $f\left(x\right)=-2\cos 3x$, maka $a=-2$ dan $k=3$.
Amplitudo grafiknya adalah $-(-a)=a=2$ dan saat $x=0^{\circ }$, nilai fungsinya adalah $f\left(0\right)=-2\cos 3\left(0\right)=-2\left(1\right)=-2$,
sehingga pilihan B, D, E tereliminasi.
Karena $k=3$, maka periode fungsinya adalah 
$\begin{array}{cc}k& =\frac{2\pi }{\text{Periode}}\\ 3& =\frac{2\pi }{\text{Periode}}\iff \text{Periode}=\frac{2}{3}\pi \end{array}$
Pada pilihan A, periode grafiknya adalah $\pi -(-\pi )=2\pi$, sedangkan pada pilihan C, periode grafiknya dapat dilihat dengan observasi berikut: dari titik $x=0$ ke titik $x=\pi$ terdapat 1,5 gelombang (1,5 lembah; 1,5 bukit), sehingga periodenya adalah $\frac{\pi -0}{1,5}=\frac{2}{3}\pi$
Jadi, grafik fungsi $f\left(x\right)=-2\cos 3x$ ditunjukkan pada pilihan C.

[collapse]

Soal Nomor 6
Fungsi yang sesuai dengan grafik berikut adalah $\cdots \cdot$

A. $f\left(x\right)=2\sin (x-\frac{\pi }{2})$
B. $f\left(x\right)=\sin (2x+\frac{\pi }{2})$
C. $f\left(x\right)=2\sin (x+\frac{\pi }{2})$
D. $f\left(x\right)=\sin (2x-\frac{\pi }{2})$
E. $f\left(x\right)=2\sin (2x+\frac{\pi }{2})$

Pembahasan

Beranjak dari grafik sinus: karena kurva bergeser (ke kiri) sejauh $\frac{\pi }{2}$, maka bentuk umum grafik fungsinya adalah $f\left(x\right)=y=a\sin k(x-c)$.
Untuk grafik ini, nilai $c$ yang menentukan pergeseran kurva adalah $-\frac{\pi }{2}$ (tandanya negatif, karena grafik bergeser ke kiri).
Dimulai dari titik $x=-\frac{\pi }{2}$ yang nilai fungsinya 0, grafik fungsi kembali bernilai $0$ dan berulang kembali di titik $x=\frac{3\pi }{2}$, sehingga periode grafik fungsinya adalah $\frac{3\pi }{2}–(-\frac{\pi }{2})=2\pi$.
Dengan demikian,
$k=\frac{2\pi }{\text{Periode}}=\frac{2\pi }{2\pi }=1$
Nilai $a$ ditentukan oleh nilai maksimum dan nilai minimum fungsi, yakni
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{2-(-2)}{2}=2\end{array}$
Jadi, rumus grafik fungsinya adalah $f\left(x\right)=2\sin 1(x+\frac{\pi }{2})=2\sin (x+\frac{\pi }{2})$
(Jawaban C)

Soal Nomor 7
Perhatikan grafik berikut.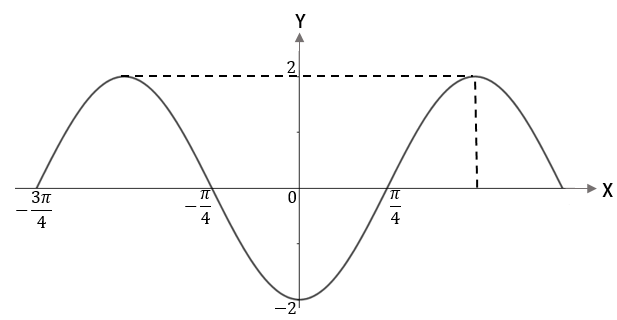

Fungsi yang memenuhi grafik di atas adalah $\cdots \cdot$
A. $f\left(x\right)=-2\sin (x-\frac{\pi }{4})$
B. $f\left(x\right)=-2\sin (x+\frac{\pi }{4})$
C. $f\left(x\right)=-2\sin (2x-\frac{\pi }{2})$
D. $f\left(x\right)=-2\sin (2x+\frac{\pi }{2})$
E. $f\left(x\right)=-2\sin (2x-\frac{\pi }{4})$

Pembahasan

Beranjak dari grafik sinus: karena kurva bergeser (ke kiri) sejauh $\frac{\pi }{4}$, maka bentuk umum grafik fungsinya adalah $f\left(x\right)=y=a\sin k(x-c)$.
Untuk grafik ini, nilai $c$ yang menentukan pergeseran kurva adalah $-\frac{\pi }{4}$.
Dimulai dari titik $x=-\frac{3\pi }{4}$ yang nilai fungsinya 0, grafik fungsi kembali bernilai $0$ dan berulang kembali di titik $x=\frac{\pi }{4}$, sehingga periode grafik fungsinya adalah $\frac{\pi }{4}–(-\frac{3\pi }{4})=\pi$.
Dengan demikian,
$k=\frac{2\pi }{\text{Periode}}=\frac{2\pi }{\pi }=2$
Nilai $a$ ditentukan oleh nilai maksimum dan nilai minimum fungsi, yakni
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{2-(-2)}{2}=2\end{array}$
Catatan: Pilihan ganda pada soal menunjukkan bahwa $a=-2$, artinya kurva sinus menurun, lalu menanjak. Ini menjadi alasan mengapa kita anggap kurva bergeser ke kiri.
Jadi, rumus grafik fungsinya adalah$$f\left(x\right)=-2\sin 2(x+\frac{\pi }{4})=-2\sin (2x+\frac{\pi }{2})$$(Jawaban D)