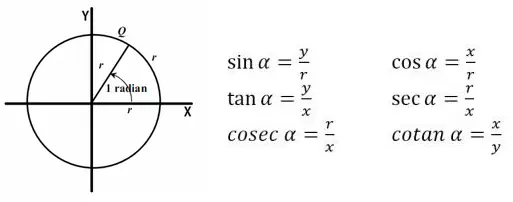Hanna Kamila Maharani

Nama : Hanna Kamila M. (17) Kelas : X IPS 3 Tanggal : 25 Januari 2021 Soal Kontekstual (Kehidupan Sehari-hari) Berkaitan dengan Perbandingan Trigonometri pada Segitiga Siku-siku  1. 2. Pada segitiga ABC lancip, diketahui cos A = 4/5 dan sin B = 12/13 maka sin C = ... a. 20/65 b. 36/65 c. 56/65 d. 60/65 e. 63/65 Pembahasan: Jika cos A = 4/5, maka: sin A = 3/5 (didapat dari segitiga siku-siku berikut ini: (cos= samping/miring, sin= depan/miring) Jika sin B = 12/13 maka cos B = 5/13 (didapat dari segitiga siku-siku berikut ini: Maka, sin C = sin A . cos B + sin B . cos A                     = 3/5 . 5/13 + 12/13 . 4/5                     = 15/65 + 48/65                     = 63/65 (E) jawaban : E 3. Jika cos β = -1/2 √3 dan sudut β terletak pada kuadran II, maka tan β = ... a. √3 b. 1/9 √3 c. 1/2 d. – 1/3 √3 e. -√3 Pembahasan: Perhatikan segitiga siku-siku berikut ini: Jika cos β = -1/2 √3 maka tan β = - 1/√3 (karena di kuadran II maka nilainya negatif) jangan lupa untuk merasionalkannya:

Nama : Hanna Kamila M. (17) Kelas : X IPS 3 Tanggal : 15 Februari 2021 IDENTITAS TRIGONOMETRI Pengertian Trigonometri Trigonometri  yaitu bagian dari ilmu matematika yang mempelajari tentang hubungan antara sisi dan sudut dari suatu segitiga serta fungsi dasar yang muncul dari relasi tersebut. Trigonometri juga identik dengan fungsi trigonometri yang meliputi  sinus (sin) ,  cosinus (cos) ,  tangen (tan) ,  cosecan (cosec) ,  secan (sec) , dan  cotangen (cotan)  yang kesemuanya itu merupakan cara untuk menentukan suatu sisi sebuah segitiga dan sudut yang terbentuk dari dua buah sisi dalam sebuah segitiga. Pengertian Identitas Trigonometri Identitas trigonometri   merupakan suatu relasi atau kalimat terbuka yang dapat memuat fungsi – fungsi trigonometri dan bernilai benar untuk setiap penggantian variabel dengan konstan anggota domain fungsinya. Kebenaran suatu relasi atau kalimat terbuka itu merupakan identitas yang perlu dibuktikan kebenarannya. Perbandingan Trigonometri Lingkaran den

Nama : Hanna Kamila M. (17) Kelas : X IPS 3 Tanggal : 8 Februari 2021 SUDUT-SUDUT BERELASI PADA KUADRAN I, II, III, IV Sudut Berelasi merupakan lanjutan dari ilmu trigonometri tentang kesebangunan pada segitiga siku-siku untuk sudut kuadran I atau sudut lancip (0 − 90°). Mari kita simak penjelasannya berikut. Rumus Sudut Berelasi Dengan memanfaatkan sudut-sudut relasi, kita dapat menghitung nilai perbandingan pada trigonometri untuk sudut pada kuadran lainnya, termasuk sudut yang lebih dari 360° dan sudut negatif. Sudut Berelasi di Kuadran I Untuk α = sudut lancip, maka (90° − α) merupakan sudut-sudut kuadran I. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut : sin (90° − α) = cos α cos (90° − α) = sin α tan (90° − α) = cot α Sudut Berelasi di Kuadran II Untuk α = sudut lancip, maka (90° + α) dan (180° − α) merupakan sudut-sudut kuadran II. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut : sin (90° + α) = cos α cos (90° + α) = -sin α tan (90° + α) = -cot α sin (